On Oct. 27, the Coding Club opened a discussion about the Collatz Conjecture, an unsolved mathematical problem that states whether repeating arithmetic operations allows numbers to eventually reach one. 

The Collatz Conjecture, the main topic of the meeting, states that if the following function is infinitely repeated, the number will eventually reach one. The function is as follows:

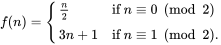
While no number has been found to go against this conjecture, it has not been proven mathematically.

Students first made a program that outputs all the iterations of the Collatz Conjecture of a given number. Then, students were given a range of numbers and modified the code to output the number of iterations needed for each given number to reach one. The data was compiled into a scatter plot.

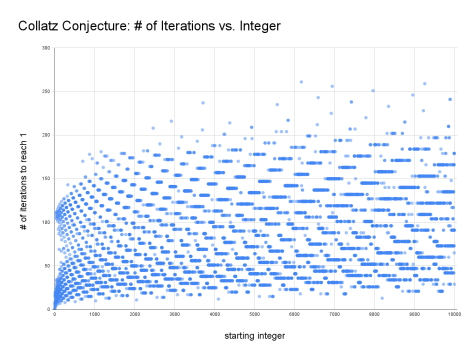
“I really liked how relaxed the atmosphere was,” Russell Jin (9), a participant of the meeting, said. “People could have fun while learning, and we did not have to be afraid of failure. The fact that this problem is so easy to understand yet difficult to solve intrigues me.” 

Coding Club executives also aided beginner programmers in coding the Collatz Conjecture such that all participants fully understood the relationship between Computer Science and Mathematics.

“The Coding Club is planning on hosting more after school sessions on various algorithms,” Jinwook Shin (12), Coding Club president said. “We are also planning on introducing club members to various fields of computer science using videos and movies that will further their interest in the subject.”